Power saturn radiates

$$P_{saturn} = 4\pi R_{Saturn}^{2}\sigma T_{Saturn}^{4}$$

First calculate with T as 76K:

$$P_{Saturn}^{T=76K} = 4\pi×57500^2×5.6703*10^{−8}×(76)^4$$
$$ = 7.8596*10^{10} W$$

Now T as 93K:

$$P_{Saturn}^{T=93K} = 4\pi×57500^2×5.6703*10^{−8}×(93)^4$$
$$ = 1.7623*10^{11}W$$

We have our two powers one $P_{Saturn}^{T=93K}$ and one $P_{Saturn}^{T=76K}$ so now we find the difference:

$$P_{difference} = P_{Saturn}^{T=76K} - P_{Saturn}^{T=93K} = 9.7634*10^{10}W$$

So Saturn radiates 0.554 times the power that saturn absorbes by sun which increases the temp to 93K.

Sun and Saturn

Some info on Sun And Saturn:


$E_{\odot} = 4\pi{}R_{\odot}^2\sigma{}T_{\odot}^4$

$E_{\odot} = 4*\pi{}*(695.508*10^6)^2*5.9703*10^-8*5777^4$
$= 3.88391*10^{26} W$

At Saturn, this energy is passing through a sphere with a radius of $R_{sphere}$, the distance between Saturn and the Sun, and the energy passing through each square metre of the sphere is given by
$Power density_\text{Rsphere} = \frac{E_{\odot}}{4\pi*R_\text{sphere}^2}$


$\text{Power density}_\text{Rsphere} = \frac{3.88391*10^{26}}{4*\pi*(9.6AU * 149.6*10^9m/AU)}$
$\text{Power density}_\text{Rsphere} = 2.152070365*10^{13}W/m^2$


$E_{absorbed}  = \pi R_{saturn}^2*Energy_{Rsphere}$

$E_{absorbed} =  \pi*(58232)^2*2.15207*10^{13}$
$E_{absorbed} = 2.2926*10^23km^2W$

Roche limit Questions

Find the roche limit of a planet with Mass $5.87*10^28Kg$ (Heehee! I love to exaggerate some things!) and me with a mass of $45Kg$. My radius is about 13cm or 0.00013km! The Formula is this for a rigid object 

Ans:
 
$M_M = 5.87*10^28Kg$

$M_m =  45Kg$

$R_m = 0.00013km$


$d = 2.44*R_m(\frac{M_M}{M_m})^\frac{1}{3}$

$d = 2.44*0.00013*(\frac{5.87*10^28}{45})^(\frac{1}{3})$

$d = 346583.8921\text{km or} 3.465*10^5 km$ #at this distance I will be the planets ring!

New question:

A supermassive star with density $7005.5Kg/m^2$ and a planets density of $1000Kg/m^2$ and $R = 47008Km$. The planet is liquidy, find the roche limit with the formula 

Ans:

$p_M = 7005.5kg.m^2$

$p_m =  1000kg/m^2$

$R = 47008Km$

$d = 2.44 * R(\frac{p_M}{p_m})^(\frac{1}{3})$

$d = 2.44 * 47008(\frac{7005.5}{1000})^(frac{1}{3})$

$d = 219469.7Km = 2.19*10^5km$

Roche limit

Roche limit is a limit at which a planet tears apart a moon or object via tidal Forces

The formula for Roche Limit for a rigid object is      

Where $M_M$ is The mass of the primary or the planet.
           $M_m$ is the mass of the secondary or moon.
           $R_m$ is the Radius of the secondry or moon.

The formula for fluid objects is     
Where $R$ is the Radius of the primary or planet
           $P_M$ is the Density of the primary or planet.
           $P_m$ is the density of the secondry or moon.


Consider an orbiting mass of fluid held together by gravity, here viewed from above the orbital plane. Far from the Roche limit the mass is practically spherical.


Closer to the Roche limit the body is deformed by tidal forces


Within the Roche limit the mass's own gravity can no longer withstand the tidal forces, and the body disintegrates.


Particles closer to the primary move more quickly than particles farther away, as represented by the red arrows.


The varying orbital speed of the material eventually causes it to form a ring.

Which is spookiest

For the new poll Which is Spookiest refer here here

Long journey

How long would it take to travel from one end of the visible Universe to the other end, if you were travelling at the different speeds ???

Ans:

  

$$1. speed = 1 Ly/sec$$

$$\text{Distance from one edge to the other}= 93*10^9Ly$$

$$ Time = \frac{distance}{speed}$$

$$ Time = \frac{93*10^9}{1} = 93*10^9seconds = 1.55*10^9min = 25.83*10^6hours$$  

$$ =1.076*10^6days = 2948.63years$$ 

Now:

$$2.speed = 1parcsec/sec$$

$$\text{distance from one edge to other}= 28*10^9parcsec$$

$$ Time = \frac{28*10^9}{1} = 28*10^9sec = 4.66*10^8min = 7.77*10^6hours = 3.2*10^5days $$

$$ = 876.712years$$

Python codes for easy work

    >>> import math
    >>> def grav_poten_energy(m1,m2,r):
                 constant = 6.672e-11
                 form = -((constant*m1*m2)/r)
                 return form

    >>> def kinetic_energy(m, v):
                  form = (1/2)*m*v**2
                  return form

    >>> def angular_momentum(m, v, R):
                  return m*v*R

    >>> def momentum(m, v):
                  return m*v

    >>> def centripetal_acceleration(v, R):
                  return (v**2/R)

    >>> def gravity(G, m, r):
                  g = 6.672e-11
                  if G != g:
                            return None
                  form = (G*m)/r**2
                  return form

    >>> def gravity_two_object(G, m1, m2, r):
                  g = 6.672e-11
                  if G != g:
                            return None
                  form = (G*m1*m2)/r**2
                  return form

     >>> def Kepler_third_law2(K, R):
                   form=(4*math.pi**2)/(K*R)
                   return form

     >>> def Kepler_third_law(K, a):
                   form = math.sqrt(K*a**3)
                   return form

      >>> def synodic_period(period1, period2):
                    form1 = (period1*period2)/(period2-period2)
                    return form1

      >>> def resolution(arcsec, distance):
                    degree = arcsec/3600
                    form2 = (math.pi/180) * distance
                    return degree*form2

      >>> def alt(zen):
                    form = 90 - zen
                    return form

       >>> def zenith(lat, dec):
                     return lat - dec

        >>> def distance(a,r):
                      form1 = a/57.3
                      main = form1 * r
                      return main

           >>> def flux(sigma, T):
                         return sigma*T**4

           >>> def luminosity(R, F):
                         return 4*math.pi*R**2*F

          >>> def doppler_effect(v, c, lambda0):
                        return lambda0*(1-(v/c))

New question related to schwarzschild radius

Sun massed black-hole?

* Q.1. Calculate the radius of a black hole that has the same Mass of Sun.

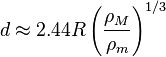
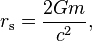Ans:            this is our Formula
$$  m =\text{ Mass of the sun} = 1.989x10^30 kg $$

  

$$ G =\text{ gravitational constant} = 6.672x10^-11 Nm^2/kg^2 $$

$$  c = 2.9979x10^8 m/s $$
so:
         
$$  R  =2 * 6.672x10^-11 * 1.989x10^30/(2.9979x10^8)^2  $$

$$  R  = (  2.65412x10^20  ) / (  8.98740441x10^16  ) $$

$$  R  = 2953.156973 m   or   2.953 km $$
              

                                 

* I am currently reading this book  "voyages through the universe ,third edition by Frankoi ,Morrison ,Wolff ",this book has some exercise which have no answers ,here I am solving the question on my own for knowledge .