Roche limit is a limit at which a planet tears apart a moon or object via tidal Forces
The formula for Roche Limit for a rigid object is
Where $M_M$ is The mass of the primary or the planet.
$M_m$ is the mass of the secondary or moon.
$R_m$ is the Radius of the secondry or moon.
The formula for fluid objects is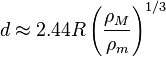
Where $R$ is the Radius of the primary or planet
$P_M$ is the Density of the primary or planet.
$P_m$ is the density of the secondry or moon.

Consider an orbiting mass of fluid held together by gravity, here viewed from above the orbital plane. Far from the Roche limit the mass is practically spherical.

Closer to the Roche limit the body is deformed by tidal forces

Within the Roche limit the mass's own gravity can no longer withstand the tidal forces, and the body disintegrates.

Particles closer to the primary move more quickly than particles farther away, as represented by the red arrows.

The varying orbital speed of the material eventually causes it to form a ring.
The formula for Roche Limit for a rigid object is

Where $M_M$ is The mass of the primary or the planet.
$M_m$ is the mass of the secondary or moon.
$R_m$ is the Radius of the secondry or moon.
The formula for fluid objects is
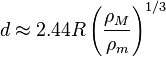
Where $R$ is the Radius of the primary or planet
$P_M$ is the Density of the primary or planet.
$P_m$ is the density of the secondry or moon.
Consider an orbiting mass of fluid held together by gravity, here viewed from above the orbital plane. Far from the Roche limit the mass is practically spherical.
Closer to the Roche limit the body is deformed by tidal forces
Within the Roche limit the mass's own gravity can no longer withstand the tidal forces, and the body disintegrates.
Particles closer to the primary move more quickly than particles farther away, as represented by the red arrows.
The varying orbital speed of the material eventually causes it to form a ring.
No comments:
Post a Comment